
虽然关于网上没有关于作者的介绍,但是不能否认这是一本好书,不然亚马逊不会卖这么高的价格。想要免费获得本书电子版吗?点击
http://www.itextbook.cn/f/book/bookDetail?bookId=0a800df934b34e48946020957659f80d下载到就是赚到!

本书介绍了数值分析的关键思想和概念。讨论重点在于如何用数值方法来表示不同的数学模型,以便借助计算机进行高效的计算和研究。从这本书中学到的知识点和方法可以应用于需要使用数值方法的其他领域。本书通过具体实例说明了实分析、线性代数和微分方程等方法的具体过程。作者之所以会选择这些方法,是因为这些方法已被证明可以为我们提供高效的算法,并且可以用于解决多种多样的应用问题。
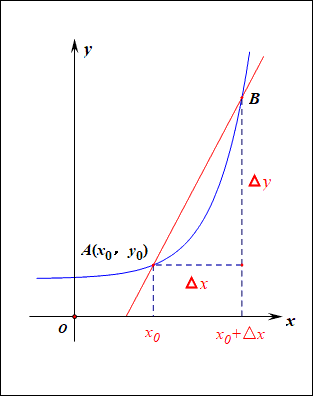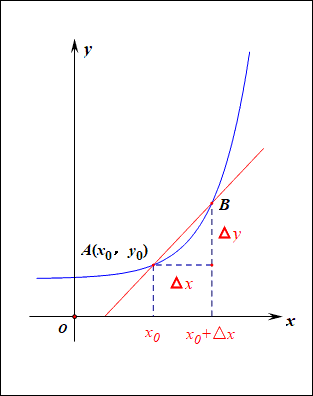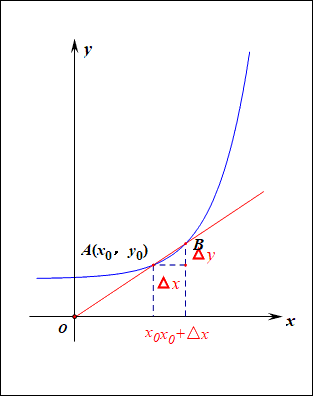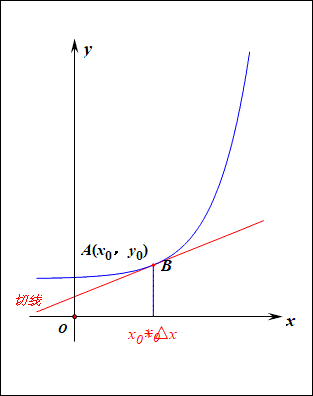
本书总共分为四个部分:函数的插值、求积,标量方程组,微分方程的有限差分法,边值问题数值解的边界方程法。针对的读者群包括数学、科学和工程专业的研究生和高年级本科生,以及一些对数值方法感兴趣的科学家和工程师。作者在本书的第一章给我们讲述了本书涉及的数值方法的基础知识,读者可以整章阅读,也可以在遇到具体问题的时候选择性地阅读,这一章的知识并不影响后面知识的贯穿性。比如书中最开始介绍了如何求微分,这个知识点很多人都有接触过,可以选择跳过,如果没有接触过也不要着急,下面这张图可以清楚地表现这个过程。
本书作为一本数学教材,一些基本的概念,比如:离散化、误差、效率、复杂性、数值稳定性、一致性、收敛性等在本书的不同位置利用不同的知识点进行了不同深度的解释和说明。除了这些基本的概念外,书中还包含了一些能让科学工作者眼前一亮的观点和知识点。例如插值法,有限元法,微分方程,边值问题等。下面简单介绍一下本书第二章讲述的代数插值的方法。插值方法是在离散数据的基础上补插连续函数,使得这条连续曲线通过全部给定的离散数据点。然后可以利用得到的插值函数估算出函数在其他点处的近似值。插值的特点是插值函数必须经过给定的插值点,下面这个例子可以很好地说明这个情况。
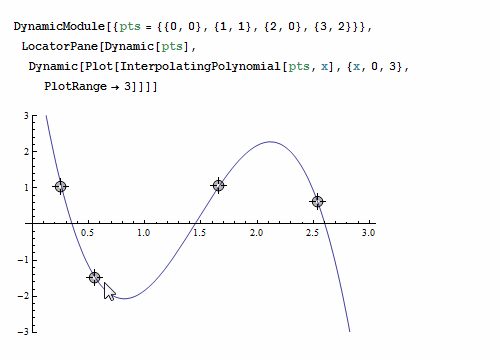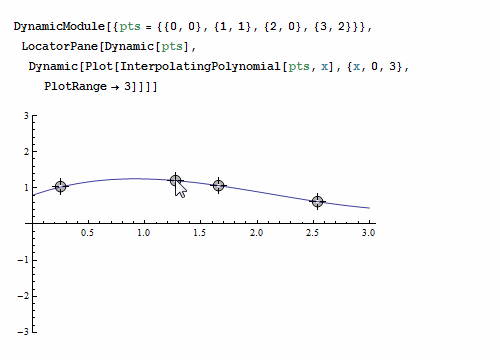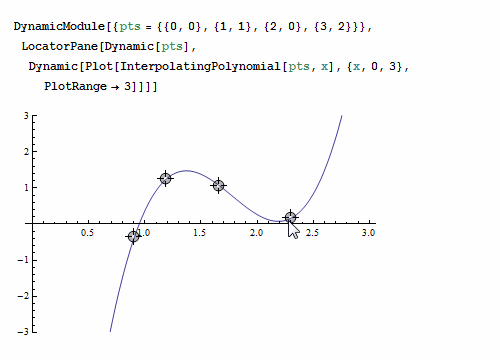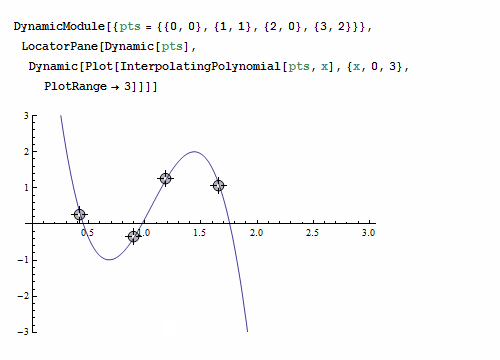
本书最大的特点是整本书都保持着严谨的数学风格,但很少使用泛函分析这类数学性很强的工具证明书中提到的方法。这种撰写方式使得这本书面向的读者范围更广,不仅仅是数学家和数学专业出身的学生。同时这还使得证明的过程不违背数学领域的的任何基础知识点。本书注重对关键知识点的解释,除了让读者知其然之外,更注重的是知其所以然。因此对于书中所有重要的数学结果都给出了严格的证明过程。同时,还提供了大量的例子来说明这些结果如何应用于个别问题的分析中去。
此外,本书没有试图描述尽可能多的、不同的方法和技巧。相反,作者只为我们讲述了有限数量的已知方法,注重的是让读者精通方法技巧,而不是贪多嚼不烂。在书的正文中,针对每种提出的方法,作者都为我们讲述了如何将这些方法运用到实际中去,在讲述的过程中注重将学科的不同分支结合在一起。此外,在章节的结尾,根据章节内容,作者还为我们提供了大量的习题,便于读者精通这些方法。习题都是从初级到高级,非常具有挑战性。
前面我们提到过,本书致力于讲述可以利用计算机求解的数学模型来方便运算和进行科学研究,不只是纸上谈兵。还等什么,赶紧去爱教材平台下载本书电子版吧!
本书的章节目录
序言
致谢
第一章简介
第一部分函数的插值,求积
第二章代数插值
第三章三角插值
第四章定积分的计算,求积
第二部分标量方程组
第五章线性代数方程组:直接方法
第六章线性方程组的迭代解法
第七章超定线性方程组:最小二乘法
第八章非线性方程组的数值解法
第三部分微分方程数值解的有限差分法
第九章常微分方程的数值解法
第十章偏微分方程的有限差分格式
第十一章不连续解及其计算方法
第十二章椭圆型问题的离散方法
第四部分边值问题数值解的边界方程法
第十三章边界积分方程与边界元法
第十四章带投影的边界方程及差分法
数字表
参考书
参考文献
索引

