作 者：MarkBreach
出版商：Palgrave Macmillan(2011)
索书号：O1 /B828 /E
书评人：宋力强， 复旦大学数学科学学院
一直以来，小编都不希望书评署名，因为写不好就会被天下人耻笑。小编这次想要尝试一种新的写法，不只是泛泛的谈书中知识点的名字，而是挑选每章中比较简单的知识点介绍一下，这样一来，读书评也能学到一些知识。之所以挑选简单的，一是可以让大部分人看懂，再就是难的小编也说不清楚。如果读者想要了解更深入的内容，就需要仔细研读书了。小编今天要讲的书是关于工程和科学中所用到的基础数学的，先来认识一下作者吧！
小编刚看到作者照片的时候，还以为他是个音乐指挥家。Mark Breach获得剑桥大学工程与自然科学硕士学位，牛津大学测地学硕士学位，以及诺丁汉特伦特大学博士学位，他曾是英国诺丁汉特伦特大学的工程测量学的首席讲师。22年来，他担任了一些硕士课程的课程项目领头人，教授研究生和本科生。他是皇家特许测量师学会成员，皇家天文学会成员，土木工程测量师学会成员，皇家航海学会副研究员。曾在国际著名杂志发表过几十篇论文，并著有多本书籍。
本书适用于高等教育学生，便于他们理解稍微困难的学科。简单来说，本书可以分为基本运算，初等代数和高等代数，几何和三角函数，微积分，概率这几部分内容。基本运算部分小编就不赘述了，这主要包括本书的前五章，主要涉及我们高中学的加减乘除，幂运算，小数运算，这部分内容看起来那是相当开心！第六章的的图表也是我们熟悉的直方图，扇形图。
在第七到十二章，主要讲述了代数的基本知识。代数我们在高中就有涉及，只是当时不叫这个名字而已。传统的代数用有字符 (变量) 的表达式进行算术运算，字符代表未知数或未定数。除了除法 (用整数除除外)，每一个表达式都是一个含有理系数的多项式，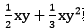
就是一个有理系数多项式。简单来说，代数就是用字母代替数字进行运算，因此我们对于数的运算规则可以平移到代数上来。比如第八章的基本运算律：加法交换律，加法结合律、乘法交换律、乘法结合律、分配律；第九、十章的三条指数律：同底数幂相乘，底数不变指数相加；幂的乘方，底数不变指数相乘；积的乘方等于乘方的积。初等代数的内容相对比较简单，读起来feel倍儿爽！
高等代数的内容就没有那么简单了，也就是本书的第二十九向量和第三十章的矩阵。向量最初被应用于物理学。很多物理量如力、速度、位移以及电场强度、磁感应强度等都是向量。由这些例子我们可以看出向量是一个既有大小又有方向的量。在介绍向量的表示之前，我们先简单介绍一下坐标系，想象一下自己跟另一半去电影院的情景，没有另一半的请想象自己去的场景，毕竟我们要关注的只是电影票。电影票的号码包括几排几座，这就是一个简单的坐标系(第二十章)。一般来说，为了定量地描述物体的位置及位置的变化，需要在参考系上建立适当的坐标系，我们生活在三维空间，能想象的也就只有三维坐标系，在大学数学中，研究对象往往超过三维。有了坐标系，我们就可以表示一个向量了。在空间直角坐标系中，也能把向量以数对形式表示，例如Oxy平面中(2,3)是一向量。刚才我们说过向量是有方向的，两个向量之间就存在夹角问题。这就需要第十三章和第十五章的三角函数。
矩阵是一个按照长方阵列排列的复数或实数集合，最早来自于方程组的系数及常数所构成的方阵。在物理学中，矩阵于电路学、力学、光学等；计算机科学中，三维动画制作也需要用到矩阵。
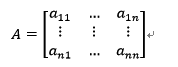
是一个矩阵。两个相同维数的矩阵相加减，就是把每个对应位置上的元素相加减；一个矩阵A乘以一个向量b，得到的是一个列向量，其第i个元素等于矩阵的第i行与向量的内积。对于矩阵矩阵乘法以及矩阵的行列式，读者还需要自己看书得到。对一些应用广泛而形式特殊的矩阵，例如稀疏矩阵和对角矩阵，有特定的快速运算算法。稀疏矩阵顾名思义就是矩阵的元素很少，也就是大多数元素为0，对角矩阵是矩阵除了对角元之外，其他的元素都是0。请原谅小编没有按照目录顺序来讲，本书顺序是环环相扣的，读者还是应该按照顺序阅读的。
本书第二十四到第二十八章讲的是微积分的基本内容。本书的微积分只涉及导数和积分以及它们的应用。一个函数在某一点的导数描述了这个函数在这一点附近的变化率。导数的本质是通过极限的概念对函数进行局部的线性逼近。例如在运动学中，物体的位移对于时间的导数就是物体的瞬时速度。直观地说，对于一个给定的正实值函数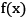
，它在一个实数区间[a,b]上的定积分
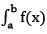可以理解为在坐标平面上，由曲线(x,f(x))，直线x=a和x=b以及x轴围成的曲边梯形的面积值。寻找已知的函数在某点的导数或其导函数的过程称为求导。反之，已知导函数也可以倒过来求原来的函数，即不定积分。应用一元函数的定积分可以解决求平面图形的面积，曲线的弧长，某项特殊几何体的体积，旋转曲面的面积等类型的问题。
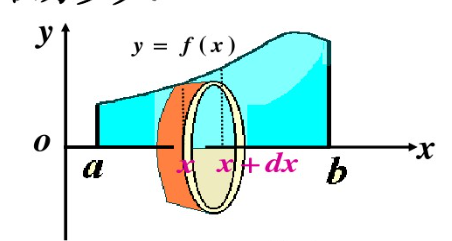
如上图所示，旋转体是由曲线y=f(x)，直线x=a，直线x=b以及x轴围城的曲边梯形绕x轴旋转一周而成。我们取[a,b]上任意小区间[x,x+dx]，取以dx为底的梯形绕x轴旋转而成的薄片的体积为体积元，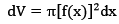
，则旋转体的体积为
。
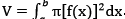概率又称为可能性，是对随机事件发生的可能性的度量，以0到1之间的实数表示一个事件发生的可能性大小。越接近1，该事件越可能发生，概率为1的事件称为必然事件；反之越接近0，则该事件越不可能发生，概率为0的事件称为不可能事件。我们都知道抛一枚硬币，正面朝上的概率为1/2，由此可以推出事件A(正面朝上)发生的概率等于事件A所包含的基本事件个数(1个正面)除以基本空间的基本事件的总个数(2，正面和反面)。古典概型还必须考虑试验结果是无限个的情况。为此可把无限个试验结果用欧式空间的某一区域S表示，假设区域S以及其中任何可能出现的小区域A都是可以度量的，其度量的大小分别用μ（S）和μ（A）表示。如一维空间的长度，二维空间的面积，三维空间的体积等。关于这些比较抽象的知识，读者还是自己探讨吧，小编真的能力有限！小编先自己鄙视自己一下！
本书最大的特点是设计布局为读者着想。本书每一章都是从简单介绍开始的，用简短的一段话告诉读者本章要讲述什么内容。每一章的文本都被分为若干部分，读者可以分批次掌握书中的知识点。根据自己的实际情况分配学习任务。书中配有大量的例子和习题，它们是书中知识点的延伸和加强，读者在阅读时应该熟练掌握。先理解书中的例子，再看抽象的数学概念也是不错的学习方法。除了每一小节后面的习题外，书中每一章都有习题，读者可以用来检验自己的学习成果。书中重要的知识点都用有颜色的框框圈出，方便读者找到重点，每一章后面的知识点总结还可以帮助读者检验是否有遗漏的知识点，这么贴心的设计，不读都对不起作者！
本书涉及的知识点都很简单，作者致力于撰写一本各个学科都可以用到的书籍，读者可以根据自己的需要选择阅读章节和阅读顺序。当然本书的知识点顺序安排是非常合理的，逐步深入。例如先将三角函数讲透彻，再来讲矩阵向量，因为后者用到了前面的知识点。欢迎大家看书后指出小编理解错误的地方，小编将不胜感激。
章节目录
1、预备知识
2、基本运算
3、小数的运算
4、幂运算
5、算数计算
6、图表
7、代数—简介
8、代数—更复杂的形式
9、代数—方程
10、代数—运用公式
11、代数—方程的变形和逆函数
12、代数—因子表示
13、几何
14、数列
15、三角函数学
16、三角函数的几何表示
17、联立方程
18、二次方程
19、固体的表面积和体积
20、坐标系
21、不规则图形
22、三角恒等式
23、对数和指数
24、微分—基本关系
25、复杂函数的微分
26、微分的应用
27、积分—基本关系
28、积分—面积和体积
29、向量
30、矩阵
31、概率
32、集中趋势和分散性