 作 者:Dr. Apoorva Khare, Prof. Anna Lachowska
作 者:Dr. Apoorva Khare, Prof. Anna Lachowska
出版商:Yale University Press; 1 (2015年11月3日)
索书号:O1-44 /K45 /E
书评人:宋力强, 复旦大学数学科学学院
美国核管理委员会处理浓缩放射性废物,是将废物放入密封性很好的圆桶中,然后扔到水深300英尺的海里,请问他们这种做法安全吗?对于这个问题,我们可以经过数学计算给出答案,想知道的一定要学好数学啊!本书是一本数学介绍书,它来自于数学课程“数学和现实世界”,上面小编举的这个例子就是用数学解决现实生活中问题。
 Dr. Apoorva Khare是印度科学院的数学助理教授,分析与概率研究小组的成员,也是斯坦福大学数学与统计学的助理研究员。他在芝加哥大学获得博士学位。他的主要研究方向是分析和组合数学,Schur多项式,曾发表过多篇论文。至于Prof. Anna Lachowska,小编只知道他于2001年毕业于耶鲁大学,除此之外,小编一无所知,Internet也一无所知。
Dr. Apoorva Khare是印度科学院的数学助理教授,分析与概率研究小组的成员,也是斯坦福大学数学与统计学的助理研究员。他在芝加哥大学获得博士学位。他的主要研究方向是分析和组合数学,Schur多项式,曾发表过多篇论文。至于Prof. Anna Lachowska,小编只知道他于2001年毕业于耶鲁大学,除此之外,小编一无所知,Internet也一无所知。
有一个问题一直困扰小编多年,作为一个数学专业的学生,我为什要学习那么多的文科内容?我想文科的学生生应该跟我有类似的困扰,为什么要学数学?当然这个问题的答案可以上升到一个很高的层次,新时代大学生要全面发展!这也正是本书的写作目的,一方面开设这样一门课程可以满足文科生的学分要求,另一方面,本书中介绍的数学知识可以让读者在以后的工作学习中受益。
Dr. Apoorva Khare和Prof. Anna Lachowska曾任教于耶鲁大学和斯坦福大学,教授“数学和现实世界”课程,基于这本课程,作者撰写了本书,目的在于以一个适当的视角将适当难度的数学呈现给大家,让非数学专业的学生感受到数学的强大与美,特别地,作者想让读者了解怎样用简单的数学理论来解决现实生活中的问题。因此本书的例子都来自于生活:人口增长模型,个人理财,匀速运动,匀加速运动,计算机安全,概率和统计。当“数学与现实世界”在耶鲁大学开设后,学生普遍反映,他们在课程中受益匪浅,他们学到了基本的数学知识,变得非常自信,很享受课程的学习过程。斯坦福大学也开设了此课程,同样反映良好。有如此贴心的作者和成功的先例,本书一定会给你不一样的惊喜。
本书的结构为(1),(2—3—4),(5—6—7—8),(9—10),(11),(12—13),(14—15—16),(17—18)。这样使得本书不管是用作教材还是自己阅读都灵活了许多。本书的目的是向读者展示怎样用简单的数学公式和技巧描述和解决数学问题。为了介绍数学知识,并把它应用到生活中去,因此知道一些规范的数学符号以及数学运算是非常必要的。本书的第一章介绍了数学中的简单运算,例如多项式的加法和乘法,解线性(或多次)方程,简化代数方程等等。同时这一章也涉及一些简单的技巧,很多复杂的数学问题通过技巧可以得到简化。我们举一个简单的例子。可以观察到这样的现象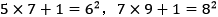
本书的第二到四章讲述了速度和加速度以及无理数。速度大家都不陌生,科学上用速度来表示物体运动的快慢。速度在数值上等于单位时间内通过的路程。加速度是描述物体速度变化快慢的物理量,其数值上等于速度变化量与发生这一变化所用时间的比值Δv/Δt。落在牛顿头上的那个苹果做的就是加速运动。本书第三章利用第一章介绍的代数基本知识,建立起物体的加速度模型,此模型可以用来描述物体在某时刻的位置和速度。这样的模型通常是二次的,其解有可能是无理数,因为要开根号。一个比较特别的无理数是黄金比例。黄金比例在造型艺术中具有美学价值,在工艺美术和日用品的长宽设计中,采用这一比值能够引起人们的美感,断臂维纳斯和蒙娜丽莎都用到了黄金比例。在实际生活中的应用也非常广泛,建筑物中某些线段的比就科学采用了黄金分割。
下面我们来看一个简单的银行存款收益模型(P85)。假设你去银行存A美元,银行以单利计算利息,利息率为r%,则每年可以收到r美元的利息,则t年之后,可以收到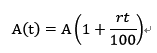
美元的利息。接下来我们来看复利模型,复利简单来说就是利滚利,复利是指在每经过一个计息期后,都要将所生利息加入本金,以计算下期的利息。同样是A美元和r%的利息率,用复利模型来算,t年后的利息为
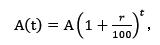 ,
,
这就是一个指数函数。如果已知利息和时间,反推利息率,就用到了对数函数的知识。本书的第五至八章主要讲述这方面的知识。
学到这些之后,我们来解决一个实际问题,假设你奶奶手里有两万块钱,想要存起来等你结婚包红包,有两种选择,一是单利5%,一是复利4.5%,存5年选择哪种存法?10年呢?
级数的概念来自于将指数增加的数求和,仍然以银行存款为例,假设银行以一个季度为单位计算复利,每年的利息为r%,存入A美元,t年之后的利息为

假设从今年开始,你每年存A美元,n年后你可以得到的钱为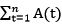
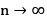
很多时候,我们并不能精确算出结果,这就需要第十一章的知识,估计近似结果。第十二、十三章是模运算,通俗来讲就是求余数。作者举了时钟的例子,请问下午10点再过16个小时是几点?10+16=26显然不合常理,因此由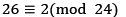 可知是下午两点。
可知是下午两点。
本书从第十六章开始,进入概率论和统计学的内容。抛硬币,掷骰子是简单的概率论模型。排列和组合经常会用到,所谓排列,就是指从给定个数的元素中取出指定个数的元素进行排序。组合则是指从给定个数的元素中仅仅取出指定个数的元素,不考虑排序。比如,一天小编囊中羞涩,可以选择两餐不吃饭,小编就有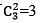 种选择,这是一个组合问题。如果小编有馒头,包子和米饭分别作为三餐,小编有
种选择,这是一个组合问题。如果小编有馒头,包子和米饭分别作为三餐,小编有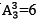 中种选择,这是一个排列问题。本书最后一部分讲述回归问题,包括数据的期望和方差,以及数学你拟合。
中种选择,这是一个排列问题。本书最后一部分讲述回归问题,包括数据的期望和方差,以及数学你拟合。
读者可以发现本书最大的特点是所有的例子均来自于现实生活,且与我们息息相关,看过就会让读者印象深刻。像第二章中的速度模型,第四章中的黄金分割,以及后面几章涉及的存款模型。所有的例子作者都做了详细的描述,而且给出了具体的解决方法。读者可以轻松地看出数学是怎样在这些例子中发挥作用的。其次作者给出例子的宗旨是让没有任何数学背景的人都可以看懂,是不是非常贴心。此外,每一章作者都给出了大量的例子,让读者不记住都有点难。
另外,本书从第二章开始都分成了两个部分,第一部分简单讲述需要的基本的数学知识,包括定义,解释等;第二部分是现实生活中的应用。两部分相辅相成,使得读者在学到抽象的数学知识后可以立马发掘它在生活中的应用,既能提升读者的阅读兴趣,又有利于理解数学知识。每一章的最后都配有大量的习题,这些习题也来自于生产生活中,加深读者对知识点的理解。总之,本书不管是作为科普读物还是数学的入门教材,都能使读者收益良多。
章节目录
前言
致谢
1、代数:计算的艺术和工艺
2、速度:在路上
3、加速度:在苹果掉落之后
4、无理数:黄金分割和其他根
5、指数:你要为曼哈顿岛付多少钱?
6、对数1:树上可以长出钱,但是需要时间
7、对数2:改变世界
8、e:成长和衰败的女王
9、有限级数:将你的债券求和
10、无限级数:分离与永恒的神话
11、估计:你的初始猜测是什么?
12、模运算1:与时钟和日历相关
13、模运算2:怎样保密?
14、概率:骰子,硬币,纸牌和连胜
15、排列与组合:计算你的选择
16、贝叶斯公式:怎样赢得一辆车或者一只羊?
17、统计:Baba Ruth 和Barry Bonds
18、回归:在大数据中找到联系
更大的故事
参考答案
附录
