
出版商:Edizioni della Normale; (2011年11月11日)
索书号:O241 /P778 /E
书评人:宋力强, 复旦大学数学科学学院

每次双十一小编剁手后,都发现其实也就优惠了几块钱。但是小编绝对的良心商家,从不收钱还保证正品!小编今天要推荐的书出版于2011年11月11日!比双十一还多了一个十一!怪不得小编只能看书不能写书,别人出书的时候我却在剁手!先来看看这个没有被某宝忽悠的人是谁。
Federico Giovanni Poloni出生于1983年(小编惊呆了,80后都出书了,而且他比小编大不到10岁),他在意大利的比萨大学获得数学学士和硕士学位,于2011年在SNS(Scuola Normale Superiore di Pisa)获得博士学位,现在是比萨大学计算机科学学院的研究员。他的主要研究方向包括:矩阵方程理论,特别是二次矩阵方程和代数Riccati方程;算法的数值解,特别是直接矩阵迭代,如循环缩减和加倍算法;应用的来源,应用概率论,排队论,控制论和计量经济学;M-矩阵,艾米特矩阵和辛矩阵,秩和位移结构等。
虽然本书的内容并不适合很多人,但是小编不得不说本书的写作方式值得大家学习,对于任何想要写论文或者写书的人来说,本书提供了一个版本。本书致力于研究二次矩阵和向量方程的求解算法,作者深入研究了不同形式的方程,这些方程出现在现实生活的很多应用中。
本书名为二次矩阵向量方程,研究对象是二次矩阵方程和二次向量方程。二次矩阵(向量)方程顾名思义,是一个以矩阵(向量)为变量的二次方程。更具体点说,本书主要处理含有N个未知量的N个二次方程组。在本书所讲的方法中把未知量看做一整个矩阵或者向量,然后再应用线性代数的技巧和方法进行求解。数值代数方法可以提供数值友好的处理办法,因此作者更喜欢将N个方程组看做关于向量或者矩阵的单个方程。不但好处理而且看起来简单方便哦!
本书中考虑的大多数方程都会假设系数是非负的,这样就可以保证方程有非负的解,有的方程的解不止一个,研究人员一般会对最小非负解感兴趣。锥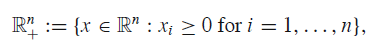
的性质,Perron-Frobenius理论和M矩阵有很重要的作用,关于这些知识点以及其他一些书中会用到的数值代数的知识点都在第一章有所介绍。阅读本书的时候,读者不必翻阅其他书籍来了解相关的知识点,因为所有需要的都在第一章介绍了,就是这么贴心!
从马尔科夫二进制树的建模中出现的一个一阶方程具有如下形式: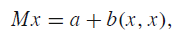
M是M-矩阵b是一个双线性型,这是一个非常普通的方程,因为很多其他的二次矩阵(向量)方程都可以表示成这种形式。本书的第二章介绍了这个方程的基本性质;同时本章还介绍了最小解,基本函数迭代的收敛性以及牛顿法。
在第三章,作者介绍了一个用于解上述二次向量方程的新算法,这个算法和传统的固定点迭代有完全不同的表现。第四章作者介绍了单边二次矩阵方程(UQME)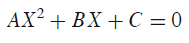
此方程和二次特征值问题有很多联系。二次特征值问题的有效解法是循环约化(CR),对数约化(LR)也是一种方法,它是从概率论中演化而成的。本章作者还阐述了CR/LR和牛顿法解二次向量方程的关系。结构化加倍算法是最近新发现的解非对称代数Riccati方程的一种方法,从矩阵束的特征值的方面来理解,并且可以应用于很多其他的方程。第五章作者主要阐述这个算法,并且给出了它和CR方法的联系。本书第六章则主要讲述如何把NAREs转化为UQMEs,并给出了数值实例。第一部分的阐述是不是跟下面这图特别像?条理清晰,环环相扣。
在第七章,作者阐述了类柯西矩阵以及它们的性质,并对现有算法进行了改进。第八章作者分别阐述了用牛顿法解不同方程的方法以及它们之间的联系。在控制理论中,很多时候都会假设矩阵是非奇异的,但是这种假设很多情况下是不成立的。本书第九章致力于求解控制理论中出现的奇异矩阵方程,叫做Lur方程。第十章介绍了SDA可能的变形,以求更准确地处理问题。
然而当矩阵收敛个数超过两个时,需要定义一个矩阵的几何均值,相信大家对数的几何均值并不陌生。这里定义的矩阵几何均值和Riemannian几何均值有很深的联系,在很多应用中,两个矩阵的几何平均值作为一个自然候选变量来表示不确定性对数值实验结果的影响。在第十一章,提出了定义矩阵几何均值的新方法。其他一些几何均值的构造方法在第十二章提出。
了解完本书内容之后,读者会发现本书从当头到尾只注重一个问题------二次矩阵(向量)方程,详细地将这个问题的来龙去脉展示在读者面前。本书提供了一种全新的写作方法,并不是所有的书籍都需要广泛涉猎,专注一个问题,将它细致地阐述给别人,同时加上自己的想法和对传统算法的改进,也会引人入胜。小伙伴们不要总盯着自己的购物车,纠结要不要清空了,还是仔细研究一下本书的行文思路,再根据本书的思路认真总结一下自己的研究内容,说不定也会在三十岁之前出版一本呢!作者在出书的时候才相信我们一定会比作者做得好,虽然小编说这话的时候没有一点底气。
阅读本书的章节目录,读者可以发现,几乎每一章都包含结论和研究方向。作者在每章结束后将这一章的主要内容总结在这一小节,供读者复习。多读类似的章节,我们可以学会归纳总结,以整体的眼光看待学术问题。同时读者可以先自己总结主要内容,然后再和作者总结的比较一下,看看自己跟出书的差距在哪里。另外书中的研究方向提出了本书内容中的不足之处,并给出了关于此课题以后可能的研究方向。朋友们要是找不到课题可以做,不防借鉴一下。本书中每个方法都配有数值例子,不但使得方法清晰明了,而且也验证了方法的可行性。
如果你也想在三十岁之前出书,一定不要错过这本教材!
章节目录
简介
第一章 线性代数基础
1.1 非负矩阵和M-矩阵
1.2 Sherman–Morrison–Woodbury 公式
1.3 牛顿法
1.4 矩阵多项式
1.5 矩阵束
1.6 无限乘积空间
1.7 Mobius 转置和 Cayley转置
1.8 控制理论专有名词
1.9 特征值分布
第一部分 二次向量和矩阵方程
第二章 二次向量等式
2.1 简介
2.2 一般问题
2.3 具体案例
2.4 最小解
2.5 函数迭代
2.6 牛顿法
2.7 改进牛顿法
2.8 最小解的正定性
2.9 其他具体案例
2.10 结论和研究方向
第三章 QVEs 的Perron向量迭代
3.1 应用
3.2 问题的假设
3.3 最优方程
3.4 Perron迭代
3.5 Perron迭代的收敛性分析
3.6 数值实例
3.7 结论和研究方向
第四章 单边二次矩阵方程
4.1 应用
4.2 算法简介循环约化
4.3 一般化推广
第五章 非对称代数Riccati方程
5.1 应用
5.2 理论性质
5.3 Schur方法
5.4 函数迭代和牛顿方法
5.5 矩阵符号方法
5.6 束算法中的块交换方法
5.7 不求逆的NMS方法
5.8 矩阵符号和圆盘迭代
5.9 结构化加倍算法
5.10 结论和研究方向
第六章 把NAREs转化为UQMEs
6.1 简介
6.2 一些假设
6.3 把NAREs转化为UQMEs
6.4 特征值转化
6.5 旧的和新的算法
6.6 数值实例
6.7 结论和研究方向
第二部分 等级结构的NAREs
第七章 类柯西矩阵的随机优化算法
7.1 简介
7.2 基本定义
7.3 GKO Schur步简介
7.4 GKO的低存储形式1
7.5 GKO的低存储形式2
7.6 用Trummer形矩阵计算
7.7 数值实例
7.8 结论和研究方向
第八章 等级结构代数Riccati方程的牛顿方法
8.1 Neutron转化方程
8.2 牛顿法
8.3 类柯西矩阵的快速高斯小区法
8.5 Lu迭代
8.5 位移方法
8.6 数值稳定
8.7 数值实例
8.8 结论和研究方向
第三部分 控制理论中的矩阵方程
第九章 Lur方程
9.1 简介
9.2 Lur方程的可解性
9.3 简化的Lur方程束
9.4 SDA的实现
9.5 数值实例
9.6 结论和研究方向
第十章 广义SDA
10.1 简介
10.2 广义SDA
10.3 数值实例
10.4 结论和研究方向
第四部分 矩阵几何均值
第十一章 一个有效的矩阵几何均值
11.1 简介
11.2 已知结果
11.3 新的矩阵几何均值
11.4 矩阵几何均值的新类别
11.5 数值实例
11.6 结论和研究方向
第十二章 构造其他矩阵几何均值
12.1 简介
12.2 矩阵几何均值的例子
12.3 拟均值和符号
12.4 由映射组成获得的均值
12.5 由极限获得的均值
12.6 数值实例
12.7 结论和研究方向
第十三章 结论
致谢
参考文献
附录

